テブナンの定理...の雑な考察

テブナンの定理はなぜ成り立つのか。手元の本に書いてないので自分で考えてみた。

なんだか、すごく間違ってる気がする。

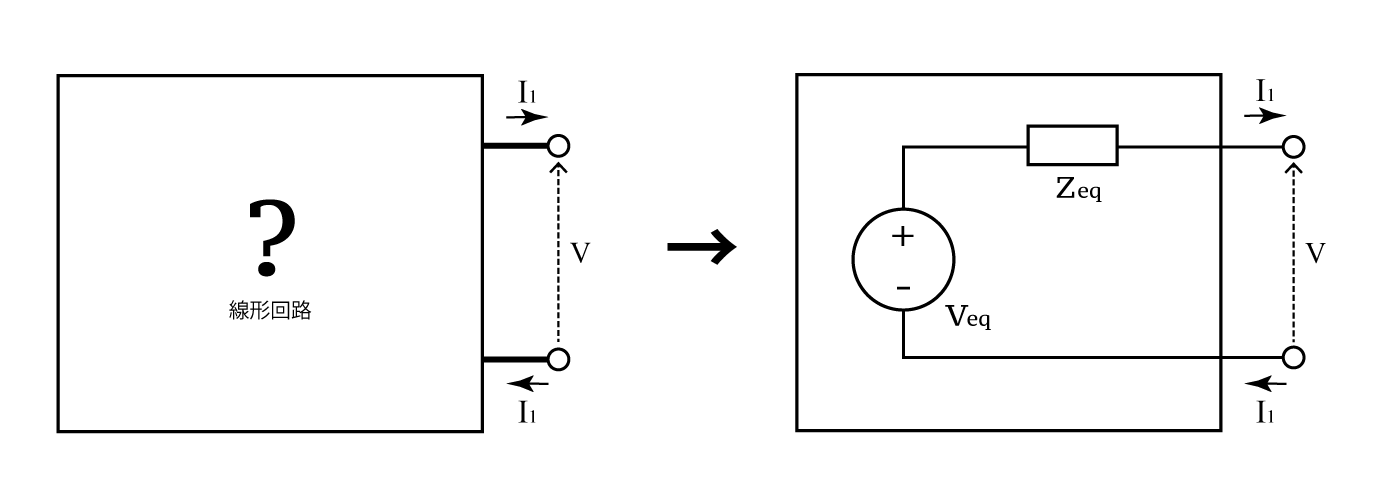
（以下正しいのかどうか分からない）

線形回路は、次の連立一次方程式で表現できる。（電流源を含む場合はダメ？）

$$Z \boldsymbol{i} = \boldsymbol{v}$$

これは次のように変形できる：

$$Z \left(\begin{matrix} \frac{1}{a} & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & \ddots & 0 \\ 0 & 0 & 0 & 1 \end{matrix}\right) \left(\begin{matrix} a & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & \ddots & 0 \\ 0 & 0 & 0 & 1 \end{matrix}\right) \boldsymbol{i} = \boldsymbol{v}$$

左辺の右側（下式）は、電流 $i_1$ の大きさをa倍することを意味する。

$$\left(\begin{matrix} a & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & \ddots & 0 \\ 0 & 0 & 0 & 1 \end{matrix}\right) \boldsymbol{i}$$

左辺の左側（下式）は、電流 $i_1$ が流れるエッジにあるインピーダンスの大きさを$\frac{1}{a}$倍することを意味する。

$$Z \left(\begin{matrix} \frac{1}{a} & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & \ddots & 0 \\ 0 & 0 & 0 & 1 \end{matrix}\right)$$

これらが意味するのは、電流 $i_1$ が流れるエッジだけを見たときに、電流 $i_1$ の大きさと、そのエッジ上にあるインピーダンス $z_1$ の大きさは反比例の関係にあるということだ。

$$z_1 i_1 = \text{const.}$$

const.の項は起電力や電圧降下の和を表しているとすると、この式は上図の等価回路を表現していることがわかる。

$$ Z_{eq} I = V_{eq} - V $$

つまり：

$$ V = V_{eq} - Z_{eq} I $$